Mean Square Error — The most used Regression loss

Step by step implementation with its gradients

3 min readDec 2, 2021

Let us start the fourth chapter — Losses and their gradients or derivatives with Mean Square error. This error is generally used if regression problems

You can download the Jupyter Notebook from here.

Back to the previous post

Back to the first post

4.1 What is Mean Square error and how to compute its gradients?

Suppose we have true values,

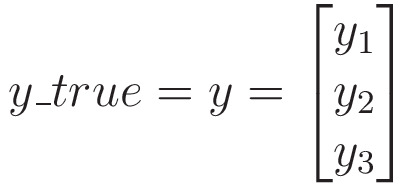
and predicted values,

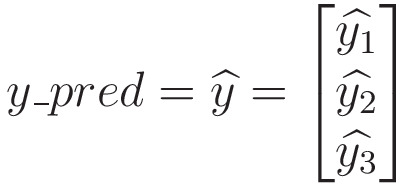
Then Mean Square Error is calculated as follow:

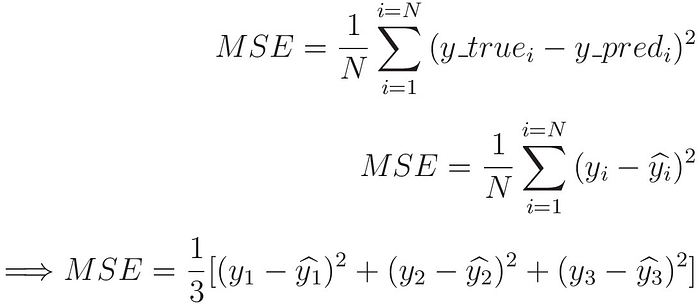
We can easily calculate Mean Square Error in Python like this.

import numpy as np                           # importing NumPy
np.random.seed(42)def mse(y_true, y_pred):                     # MSE
    return np.mean((y_true - y_pred)**2)

Now, we know that

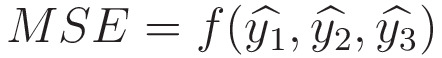
So, like the Softmax activation function, we have a Jacobian for MSE.

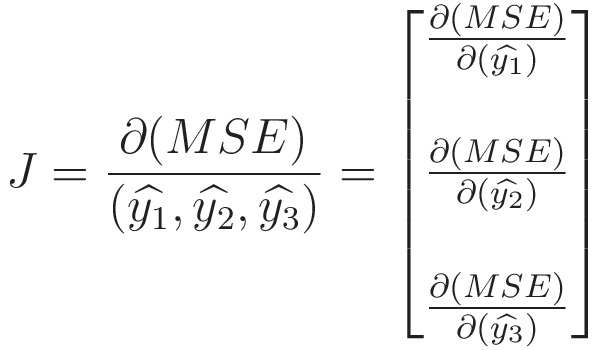
We can easily find each term in this Jacobian.

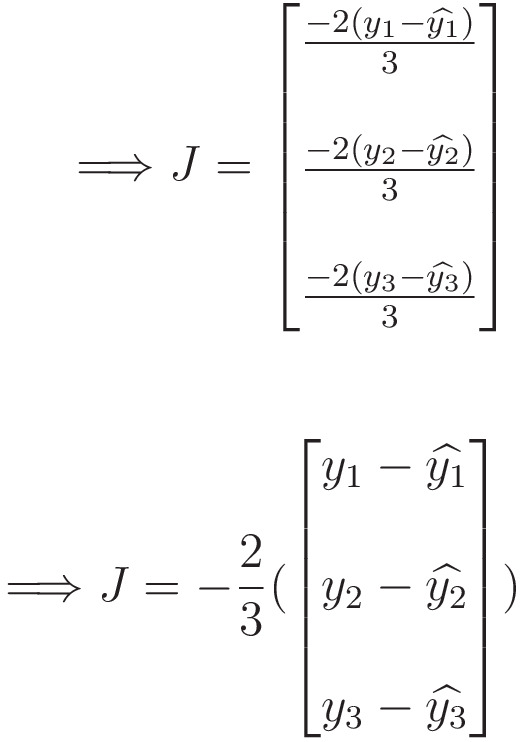
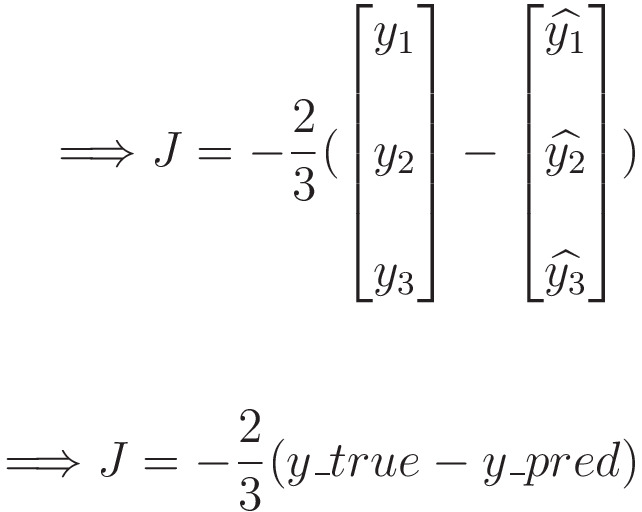
Note — Here, 3 represents ‘N’, i.e., the entries in y_true and y_pred

We can easily define the MSE Jacobian in Python like this.

def mse_grad(y_true, y_pred):                # MSE Jacobian
    
    N = y_true.shape[0]
    
    return -2*(y_true - y_pred)/N

Let us have a look at an example.

y_true = np.array([[1.5], [0.2], [3.9], [6.2], [5.2]])
y_truey_pred = np.array([[1.2], [0.5], [3.2], [4.2], [3.2]])
y_pred

mse(y_true, y_pred)mse_grad(y_true, y_pred)

I hope you now understand how to implement Mean Square Error.

Watch the video on youtube and subscribe to the channel for videos and posts like this.
Every slide is 3 seconds long and without sound. You may pause the video whenever you like.
You may put on some music too if you like.

The video is basically everything in the post only in slides.